Ока­зы­ва­ет­ся во­все не обя­за­тель­но встав­лять -ов­скую ма­те­ма­ти­ку в вебе та­к­же как это де­ла­лось в 1999 году — в виде ги­фов с про­зрач­ным фо­ном. Бу­ду­щее уже дав­но на­сту­пи­ло, те­перь мож­но ис­поль­зо­вать век­тор­ный SVG.

Это я вот к чему. Недав­но, об­за­ве­дясь Мак­бу­ком с Reti­na-дис­пле­ем про­бле­ма раст­ро­вой гра­фи­ки в вебе у меня всплы­ла в пол­ный рост: если рань­ше, ко­гда часть ка­кой-ни­будь стра­нич­ки была от­ри­со­ва­на, ска­жем, фо­то­шо­пом, а часть сред­ства­ми CSS, то про­сто глаз слег­ка спо­ты­кал­ся на этой раз­ни­це, но тер­пи­мо было. А на ре­тине раз­ни­ца ста­но­вит­ся уже жут­кой — раст­ро­вые ча­сти сай­тов вы­гля­дят как на­бор боль­ших пик­се­лей.

И если на дру­гих сай­тах это про­бле­мы их со­зда­те­лей, то на моем соб­ствен­ном бло­ге (да, да, пишу я в него реже чем ко­вы­ряю его дви­жок и ди­зайн) меня та­кая раз­ни­ца не устра­и­ва­ла со­вер­шен­но, и боль­ше все­го у меня она вид­на как раз на встав­лен­ных ма­те­ма­ти­че­ских фор­му­лах.

По­лез раз­би­рать­ся как бы ма­те­ма­ти­ку в SVG рен­де­рить, ока­за­лось что че­ло­ве­че­ство эту про­бле­му дав­но ре­ши­ло, и есть ути­лит­ка dvisvgm ров­но для это­го и пред­на­зна­чен­ная. Я вы­зы­ваю ее так:

latex some.tex
dvisvgm --no-fonts some.dvi

Все, на вы­хо­де some.svg за­ме­ча­тель­но вы­гля­дя­щий на ре­тине.

На­гляд­ная раз­ни­ца меж­ду рас­тром и век­то­ром для ма­те­ма­ти­ки (при­вет всем вла­дель­цам ре­ти­на-дис­пле­ев). Растр:

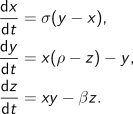
Век­тор:

Кста­ти, чтоб два раза не вста­вать, сэко­ном­лю кому-ни­будь пару ча­сов на раз­би­ра­тель­ство. У всей ма­те­ма­ти­ки у меня в бло­ге вот та­кой шаб­лон:

1
2
3
4
5
6
7
8
9

\documentclass[12pt]{article}
\pagestyle{empty}
\usepackage{amsmath}
\usepackage{sfmath}
\begin{document}

$E=mc^2$

\end{document}

Раз­вле­ка­юсь с ани­ма­ци­ей на HTML5 can­vas. На­пи­сал вот та­кую чу­дес­ную ви­зу­а­ли­за­цию ат­трак­то­ра Ло­рен­ца:

От­крыть в но­вом окне

При от­кры­ва­нии в но­вом окне, не за­будь­те что бра­у­зер мож­но пе­ре­ве­сти в пол­но­экран­ный ре­жим, на­жав F11. Так смот­рит­ся ещё луч­ше.

То что вы тут ви­ди­те, пред­став­ля­ет со­бой ани­ма­цию ре­ше­ния си­сте­мы сле­ду­ю­щих диф­фе­рен­ци­аль­ных урав­не­ний:

Где , , — те­ку­щее со­сто­я­ние си­сте­мы, — вре­мя, , , — па­ра­мет­ры си­сте­мы.

В моём при­ме­ре:

Для каж­дой ли­нии (пред­став­ля­ю­щей со­бой от­дель­ное ре­ше­ния урав­не­ния) я вы­би­раю на­чаль­ное зна­че­ние с до­бав­ле­ни­ем неболь­шо­го слу­чай­но­го чис­ла. Та­ким об­ра­зом очень хо­ро­шо за­ме­тен «эф­фект ба­боч­ки»: незна­чи­тель­ное воз­му­ще­ние си­сте­мы («взмах кры­ла ба­боч­ки») при­во­дят к очень боль­шим из­ме­не­ни­ям в даль­ней­шем, ли­нии «вы­ле­та­ю­щие» из очень близ­ких то­чек вско­ре на­чи­на­ют де­мон­стри­ро­вать со­вер­шен­но раз­ное по­ве­де­ние.

Со­всем-со­всем недав­но (мень­ше года на­зад!), был от­крыт очень ин­те­рес­ный но­вый фрак­тал — Ман­дель­буль­ба (Man­del­bulb). От­кры­ли его два ма­те­ма­ти­ка: Да­ни­эль Уайт (Daniel White) и Поль Ни­лан­дер (Paul Ny­lan­der). Они ис­поль­зо­ва­ли ги­пер­ком­плекс­ную ал­геб­ру, ос­но­ван­ную на сфе­ри­че­ской си­сте­ме ко­ор­ди­нат. Ал­геб­ра опе­ри­ру­ет трёх­эле­мент­ны­ми чис­ла­ми, со­от­вет­ству­ю­щи­ми ко­ор­ди­на­там точ­ки в трех­мер­ном про­стран­стве. Для этих чи­сел (вида ) опре­де­ле­ны опе­ра­ции воз­ве­де­ния в сте­пень:

где

И опе­ра­ция по­эле­мент­но­го сло­же­ния.

С по­мо­щью этих двух опе­ра­ций мож­но по­стро­ить трех­мер­ный ана­лог мно­же­ства Ман­дель­бро­та, вос­поль­зо­вав­шись из­вест­ной фор­му­лой , где и — чис­ла в на­шей ал­геб­ре. Трех­мер­ная точ­ка при­над­ле­жит мно­же­ству, если про­цесс для оста­ет­ся огра­ни­чен­ным (не «уле­та­ет» в бес­ко­неч­ность). При ре­а­ли­за­ции сле­ду­ет об­ра­тить вни­ма­ние, что для вы­чис­ле­ния необ­хо­ди­мо ис­поль­зо­вать двух­ар­гу­мент­ную функ­цию atan2(a,b), ко­то­рая есть прак­ти­че­ски в лю­бом рас­про­стра­нен­ном язы­ке про­грам­ми­ро­ва­ния.

Ниже при­ве­де­на моя кар­тин­ка для ман­дель­буль­бы 8-го по­ряд­ка при 5 ите­ра­ци­ях, на­ри­со­ва­на с по­мо­щью очень про­сто­го трас­си­ров­щи­ка лу­чей:

Па­ра­мет­ри­че­ские по­верх­но­сти страсть как хо­ро­ши!

Обои для ра­бо­че­го сто­ла с этой кар­тин­кой

Спе­ци­аль­но для фа­на­тов ма­те­ма­ти­ки, фор­му­ла этой по­верх­но­сти:

(далее...)

Это ста­тья по­свя­ще­на про­стым чис­лам и эф­фек­тив­ным спо­со­бам их вы­чис­ле­ния. Сра­зу ска­жу, что те ал­го­рит­мы, ко­то­рые тут при­ве­де­ны, яв­ля­ют­ся весь­ма и весь­ма нетри­ви­аль­ны­ми и са­мо­му мне не да­ва­лись до­воль­но дол­го, но в ито­ге я их всё-таки при­ду­мал, на­пи­сал и спе­шу по­де­лить­ся со все­ми вами. Ис­ход­ные тек­сты в ста­тье бу­дут при­ве­де­ны на язы­ках C# и Haskell.

Про­стое чис­ло – это на­ту­раль­ное чис­ло боль­ше еди­ни­цы, ко­то­рое име­ет ров­но два де­ли­те­ля: еди­ни­цу и само это чис­ло.

Ре­ше­то Эра­то­сфе­на – древ­ний, но при этом весь­ма эф­фек­тив­ный и до сих пор ши­ро­ко ис­поль­зу­е­мый ал­го­ритм по­ис­ка всех про­стых чи­сел не пре­вос­хо­дя­щих неко­то­ро­го N.

За­пи­шем под­ряд все чис­ла от 2 до N. Даль­ше вы­черк­нем из это­го спис­ка все чис­ла крат­ные 2, ис­клю­чая саму двой­ку, по­том вы­черк­нем все чис­ла крат­ные 3, ис­клю­чая само чис­ло 3, чис­ло 4 уже вы­черк­ну­то, вы­чер­ки­ва­ем чис­ла крат­ные 5 и т.д. Про­дол­жа­ем этот про­цесс, пока квад­рат оче­ред­но­го чис­ла не пре­вы­сит N.

Са­мая про­стая про­грамм­ная ре­а­ли­за­ция это­го ал­го­рит­ма вы­гля­дит сле­ду­ю­щим об­ра­зом:

(далее...)